Triangular bipyramid
| Triangular bipyramid | |
|---|---|
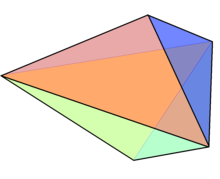 | |
| Type | Bipyramid Deltahedra Johnson J11 – J12 – J13 |
| Faces | 6 triangles |
| Edges | 9 |
| Vertices | 5 |
| Vertex configuration | |
| Symmetry group | |
| Dihedral angle (degrees) | As a Johnson solid:
|
| Dual polyhedron | triangular prism |
| Properties | convex, composite, face-transitive |
A triangular bipyramid is a hexahedron with six triangular faces constructed by attaching two tetrahedra face-to-face. The same shape is also known as a triangular dipyramid[1][2] or trigonal bipyramid.[3] If these tetrahedra are regular, all faces of a triangular bipyramid are equilateral. It is an example of a deltahedron, composite polyhedron, and Johnson solid.
Many polyhedra are related to the triangular bipyramid, such as similar shapes derived from different approaches and the triangular prism as its dual polyhedron. Applications of a triangular bipyramid include trigonal bipyramidal molecular geometry which describes its atom cluster, a solution of the Thomson problem, and the representation of color order systems by the eighteenth century.
Special cases
[edit]As a right bipyramid
[edit]Like other bipyramids, a triangular bipyramid can be constructed by attaching two tetrahedra face-to-face.[2] These tetrahedra cover their triangular base, and the resulting polyhedron has six triangles, five vertices, and nine edges.[3] A triangular bipyramid is said to be right if the tetrahedra are symmetrically regular and both of their apices are on a line passing through the center of the base; otherwise, it is oblique.[4][5]

According to Steinitz's theorem, a graph can be represented as the skeleton of a polyhedron if it is a planar (the edges of the graph do not cross, but intersect at the point) and three-connected graph (one of any two vertices leaves a connected subgraph when removed). A triangular bipyramid is represented by a graph with nine edges, constructed by adding one vertex to the vertices of a wheel graph representing tetrahedra.[6][7]
Like other right bipyramids, a triangular bipyramid has three-dimensional point-group symmetry, the dihedral group of order twelve: the appearance of a triangular bipyramid is unchanged as it rotated by one-, two-thirds, and full angle around the axis of symmetry (a line passing through two vertices and the base's center vertically), and it has mirror symmetry with any bisector of the base; it is also symmetrical by reflection across a horizontal plane.[8] A triangular bipyramid is face-transitive, or isohedral.[9]
As a Johnson solid
[edit]
If the tetrahedra are regular, all edges of a triangular bipyramid are equal in length and form equilateral triangular faces. A polyhedron with only equilateral triangles as faces is called a deltahedron. There are eight convex deltahedra, one of which is a triangular bipyramid with regular polygonal faces.[1] A convex polyhedron in which all of its faces are regular polygons is the Johnson solid, and every convex deltahedron is a Johnson solid. A triangular bipyramid with regular faces is numbered as the twelfth Johnson solid .[10] It is an example of a composite polyhedron because it is constructed by attaching two regular tetrahedra.[11][12]
A triangular bipyramid's surface area is six times that of each triangle. Its volume can be calculated by slicing it into two tetrahedra and adding their volume. In the case of edge length , this is:[12]
The dihedral angle of a triangular bipyramid can be obtained by adding the dihedral angle of two regular tetrahedra. The dihedral angle of a triangular bipyramid between adjacent triangular faces is that of the regular tetrahedron: 70.5 degrees. In an edge where two tetrahedra are attached, the dihedral angle of adjacent triangles is twice that: 141.1 degrees.[13]
Related polyhedra
[edit]
Some types of triangular bipyramids may be derived in different ways. The Kleetope of a polyhedron is a construction involving the attachment of pyramids. A triangular bipyramid's Kleetope can be constructed from a triangular bipyramid by attaching tetrahedra to each of its faces, replacing them with three other triangles; the skeleton of the resulting polyhedron represents the Goldner–Harary graph.[14][15] Another type of triangular bipyramid results from cutting off its vertices, a process known as truncation.[16]
Bipyramids are the dual polyhedron of prisms. This means the bipyramids' vertices correspond to the faces of a prism, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other; doubling it results in the original polyhedron. A triangular bipyramid is the dual polyhedron of a triangular prism, and vice versa.[17][3] A triangular prism has five faces, nine edges, and six vertices, with the same symmetry as a triangular bipyramid.[3]
Applications
[edit]
The Thomson problem concerns the minimum energy configuration of charged particles on a sphere. A triangular bipyramid is a known solution in the case of five electrons, placing vertices of a triangular bipyramid within a sphere.[18] This solution is aided by a mathematically rigorous computer.[19]
A chemical compound's trigonal bipyramidal molecular geometry may be described as the atom cluster of a triangular bipyramid. This molecule has a main-group element without an active lone pair, described by a model which predicts the geometry of molecules known as VSEPR theory.[20] Examples of this structure include phosphorus pentafluoride and phosphorus pentachloride in the gaseous phase.[21]
In color theory, the triangular bipyramid was used to represent the three-dimensional color-order system in primary colors. German astronomer Tobias Mayer wrote in 1758 that each of its vertices represents a color: white and black are the top and bottom axial vertices, respectively, and the rest of the vertices are red, blue, and yellow.[22][23]
References
[edit]- ^ a b Trigg, Charles W. (1978). "An infinite class of deltahedra". Mathematics Magazine. 51 (1): 55–57. doi:10.1080/0025570X.1978.11976675. JSTOR 2689647. MR 1572246.
- ^ a b Rajwade, A. R. (2001). Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. p. 84. doi:10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4.
- ^ a b c d King, Robert B. (1994). "Polyhedral Dynamics". In Bonchev, Danail D.; Mekenyan, O.G. (eds.). Graph Theoretical Approaches to Chemical Reactivity. Springer. doi:10.1007/978-94-011-1202-4. ISBN 978-94-011-1202-4.
- ^ Niu, Wenxin; Xu, Guobao (2011). "Crystallographic control of noble metal nanocrystals". Nano Today. 6 (3): 265–285. doi:10.1016/j.nantod.2011.04.006.
- ^ Alexandrov, Victor (2017). "How many times can the volume of a convex polyhedron be increased by isometric deformations?". Beiträge zur Algebra und Geometrie. 58 (3): 549–554. arXiv:1607.06604. doi:10.1007/s13366-017-0336-8.
- ^ Tutte, W. T. (2001). Graph Theory. Cambridge University Press. p. 113. ISBN 978-0-521-79489-3.
- ^ Sajjad, Wassid; Sardar, Muhammad S.; Pan, Xiang-Feng (2024). "Computation of resistance distance and Kirchhoff index of chain of triangular bipyramid hexahedron". Applied Mathematics and Computation. 461: 1–12. doi:10.1016/j.amc.2023.128313. S2CID 261797042.
- ^ Alexander, Daniel C.; Koeberlin, Geralyn M. (2014). Elementary Geometry for College Students (6th ed.). Cengage Learning. p. 403. ISBN 978-1-285-19569-8.
- ^ McLean, K. Robin (1990). "Dungeons, dragons, and dice". The Mathematical Gazette. 74 (469): 243–256. doi:10.2307/3619822. JSTOR 3619822. S2CID 195047512.
- ^ Uehara, Ryuhei (2020). Introduction to Computational Origami: The World of New Computational Geometry. Springer. doi:10.1007/978-981-15-4470-5. ISBN 978-981-15-4470-5. S2CID 220150682.
- ^ Timofeenko, A. V. (2009). "Convex Polyhedra with Parquet Faces" (PDF). Docklady Mathematics. 80 (2): 720–723. doi:10.1134/S1064562409050238.
- ^ a b Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
- ^ Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/cjm-1966-021-8. MR 0185507. S2CID 122006114. Zbl 0132.14603.
- ^ Grünbaum, Branko (1967). Convex Polytopes. Wiley Interscience. p. 357.. Same page, 2nd ed., Graduate Texts in Mathematics 221, Springer-Verlag, 2003, ISBN 978-0-387-40409-7.
- ^ Ewald, Günter (1973). "Hamiltonian circuits in simplicial complexes". Geometriae Dedicata. 2 (1): 115–125. doi:10.1007/BF00149287. S2CID 122755203.
- ^ Haji-Akbari, Amir; Chen, Elizabeth R.; Engel, Michael; Glotzer, Sharon C. (2013). "Packing and self-assembly of truncated triangular bipyramids". Phys. Rev. E. 88 (1): 012127. arXiv:1304.3147. Bibcode:2013PhRvE..88a2127H. doi:10.1103/physreve.88.012127. PMID 23944434. S2CID 8184675..
- ^ Sibley, Thomas Q. (2015). Thinking Geometrically: A Survey of Geometries. Mathematical Association of American. p. 53. ISBN 978-1-939512-08-6.
- ^ Sloane, N. J. A.; Hardin, R. H.; Duff, T. D. S.; Conway, J. H. (1995), "Minimal-energy clusters of hard spheres", Discrete & Computational Geometry, 14 (3): 237–259, doi:10.1007/BF02570704, MR 1344734, S2CID 26955765
- ^ Schwartz, Richard Evan (2013). "The Five-Electron Case of Thomson's Problem". Experimental Mathematics. 22 (2): 157–186. doi:10.1080/10586458.2013.766570. S2CID 38679186.
- ^ Petrucci, R. H.; Harwood, W. S.; Herring, F. G. (2002). General Chemistry: Principles and Modern Applications (8th ed.). Prentice-Hall. pp. 413–414. ISBN 978-0-13-014329-7. See table 11.1.
- ^ Housecroft, C. E.; Sharpe, A. G. (2004). Inorganic Chemistry (2nd ed.). Prentice Hall. p. 407. ISBN 978-0-13-039913-7.
- ^ Kuehni, Rolf G. (2003). Color Space and Its Divisions: Color Order from Antiquity to the Present. John & Sons Wiley. p. 53. ISBN 978-0-471-46146-3.
- ^ Kuehni, Rolf G. (2013). Color: An Introduction to Practice and Principles. John & Sons Wiley. p. 198. ISBN 978-1-118-17384-8.









